MATEMATICAS IV: BLOQUE 1: RECONOCE Y REALIZA OPERACIONES CON DISTINTOS TIPOS DE FUNCIONES

* FUNCIONES *

En matemáticas se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. algunas funciones que hay son las siguientes:

+función Trigonométrica
+Función Cuadrática
+Función Afín (Lineal)
+Función Logarítmica
+Función Exponencial
+Función Polinómica

EJEMPLOS:

	−2 → +4,	−1 → +1,	±0 → ±0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

..,

Estación → E,

Museo → M,

Arroyo → A,

Rosa → R,

Avión → A,

...

f: A → B

a → f(a),

f: Z → N

k → k², o sencillamente f(k) = k²;

g: V → A

p → Inicial de p;

V = {Palabras del español} y A = {Alfabeto español}.

Lunes → Martes, Martes → Miércoles,..., Domingo → Lunes

f: R → R, con f(x) = x³ para cada número real x.

g: R \ {0} → R, con g(x) = 1/x para cada x real y no nulo.

γ: M → G, donde γ(m) = Género de m, para cada mamífero conocido m.

A: T → R, y entonces A(t) = Área de t = B · H/2, donde t es un triángulo del plano, B su base, y H su altura.

funcion real:
f: R → R

funcion compleja:
f: C → C

funcion escalar:

f: Rⁿ → R

funcion vectorial:

f: Rⁿ → R^m

EJEMPLO..

Suponga que el conjunto A (de salida) es A = {1, 2, 3} y que el conjunto B (de llegada) es B = {0, 4, 6, 8, 10, 12} y que la relación de dependencia o correspondencia entre A y B es "asignar a cada elemento su cuádruplo".

Vamos a examinar si esta relación es una función de A en B y determinaremos dominio y recorrido.

Veamos:

A los elementos 1, 2 y 3 del conjunto A les corresponden, respectivamente, los elementos 4, 8 y 12 del conjunto B. Como a cada elemento de A le corresponde un único elemento de Y, la relación de dependencia es una función (función de A en B).

Dominio = {1, 2, 3} Recorrido = {4, 8, 12}

Notar que el recorrido es un subconjunto del codominio B = {0, 4, 6, 8, 10, 12}

Aquí debemos recordar que toda función es una relación, pero no todas las relaciones son funciones. Como ejemplos de relaciones que son funciones y algunas que no lo son, veamos las siguientes:

Si tenemos los conjuntos

A = {1; 2; 3; 4}, B = {1; 2; 3; 4; 5}

Podemos establecer las relaciones

f = { (1; 2); (2; 3); (3; 4); (4; 5) }

g = { (1; 2); (1; 3); (2; 4); (3; 5); (4; 5) }

h = { (1; 1); (2; 2); (3; 3) }:

Está claro que f, g y h son relaciones de A en B, pero sólo f es una función (todos los elementos del conjunto A tiene su correspondiente elemento en b); g no es función ya que (1; 2) y (1; 3) repiten un elemento del dominio (el 1). Tampoco h es una función ya que Dom(h) = {1; 2; 3} ≠ A (falta el 4).

EJEMPLO....

EJEMPLO...

EJEMPLO....

EJEMPLO...

Consideremos nuevamente el conjunto $\mathbb{N}\times\mathbb{N}=\ensuremath{\{\,{(a,b)}\mid {a,b\in\mathbb{N}}\,\}}$ de parejas ordenadas de números naturales y definamos la siguiente relación de equivalencia en él:

$\displaystyle (a,b)\sim (c,d)$ si y sólo si $\displaystyle \qquad a+d=b+c.$

Analicemos la clase de equivalencia de las parejas

$\displaystyle [(2,0)]$ $\displaystyle =\{(2,0),(3,1),(4,2),(5,3),(6,4),(7,5),(8,6),(9,7)\dots\},$
$\displaystyle [(7,7)]$ $\displaystyle =\{(0,0),(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(7,7)\dots\},$

EJEMPLO...

Dada una función cualquiera f : A → B se tiene:

$\begin{align} &f\circ \text{id}_A = f\\ &\text{id}_B \circ f=f \end{align}$

*RELACIONES*

La enumeración de algunos de los elementos de los conjuntos .Una relacion binaria es una relación entre dos conjuntos.

EJEMPLOS:

*Diagrama:
1 --------> 1 2 ------> 3

               2 --------> 4    4 ------> 1

3 --------> 9                  5-------> 2
               4 --------> 16                                  x-------> x²

                                                 *Ecuacion : f(x) = x²

* B = {0, 4, 6, 8, 10, 12} * Dominio = {1, 2, 3}     * Recorrido = {4, 8, 12}


    * f = { (1; 2); (2; 3); (3; 4); (4; 5) }

      * g = { (1; 2); (1; 3); (2; 4); (3; 5); (4; 5) }

       * h = { (1; 1); (2; 2); (3; 3) }:

       * X = {−4, −1, 0, 4, 9},     * Y = {−4,−3, −2, −1, 0, 1, 2, 3, 4}



     *Tabla:

Conjunto X	Conjunto Y
Ángela	55
Pedro	88
Manuel	62
Adrián	88
Roberto	90

Funciones

Inyectiva

No inyectiva

Sobreyectiva


Biyectiva

No sobreyectiva

*Grafica

*DOMINIO*

Es el conjunto de valores para los que una determinada función matemática está definida.

Lo que puede entrar en una función se llama el dominio
EJEMPLOS:

*CONTRADOMINIO*

Son el conjunto de valores que puede tomar la variable depende de la "y".

Lo que es posible que salga de una función se llama el codominio

EJEMPLOS:

*IMAGEN *

Son todos los puntos de la grafica de la funcion a los que les corresponde un valor en "y".

Lo que en realidad sale de una función se llama rango o imagen
EJEMPLOS:

MATEMATICAS IV

lunes, 22 de abril de 2013

BLOQUE 1: RECONOCE Y REALIZA OPERACIONES CON DISTINTOS TIPOS DE FUNCIONES

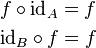
No hay comentarios:

Publicar un comentario

Datos personales